Visual Paradigm 教程[UML]:如何创建因果图?
本文共 699 字,大约阅读时间需要 2 分钟。
1943年,东京大学的Kaoru Ishikawa博士首次使用因果图或鱼骨图。该图用于识别可能导致问题的所有有根本原因。 该方法可用于任何类型的问题,并且可由用户定制以适应环境。
一、创建因果图的步骤
以下步骤概述了创建因果图时要采取的主要步骤。
- 将效果写在页面右侧的框中。
- 在效果的左侧绘制一条水平线。
- 确定效果的原因类别。 经典鱼骨图中有用的原因类别包括材料,方法,设备,环境和人。
- 考虑类别的另一种方法是根据流程中每个主要步骤的原因。
- 在水平线上方和下方绘制对角线(这些是“鱼骨”),并使用您选择的类别进行标注。
- 生成每个类别的原因列表。
- 列出每个鱼骨上的原因,绘制分支骨骼以显示原因之间的关系。
- 通过询问“为什么?”来发展原因,直到达到有用的细节水平 - 也就是说,当原因具体到能够测试变化并测量其影响时。
二、创建因果图
-
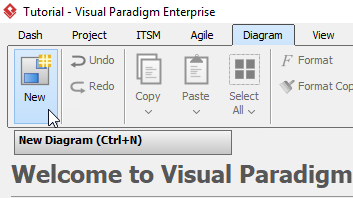
单击工具栏中的Diagram> New。
-
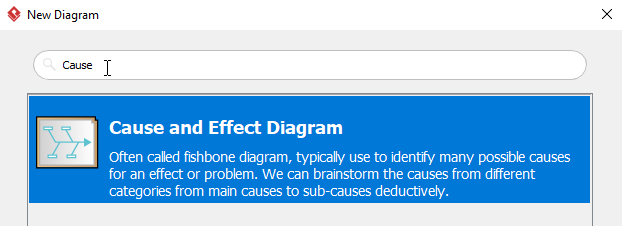
在New Diagram窗口中,选择Cause and Effect Diagram,然后单击next。您可以使用搜索栏搜索图表。
-
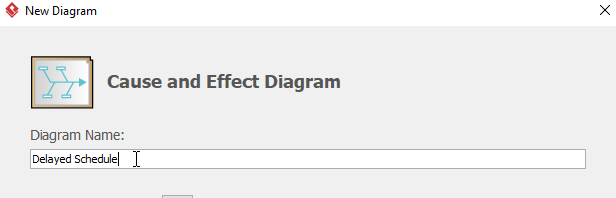
为图表命名(例如:延迟计划),然后单击“确定”以完成图表的创建。
-
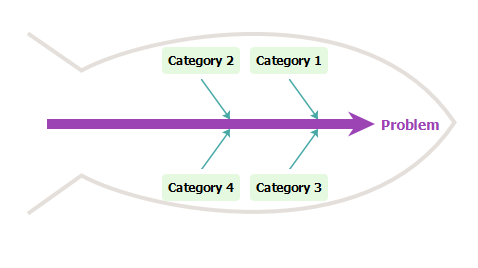
然后,您将看到如下图:
-
双击图右侧的问题并重命名(例如:Delayed Schedule)。

-
双击Category1将类别重命名为Equipment。
-
右键单击设备,然后从工具栏中选择添加主要原因以创建新的主要原因。
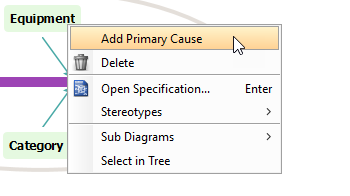
-
双击原因并将其重命名为未按时提供设备,然后通过右键单击创建次要原因未按时提供设备并选择添加次要原因。
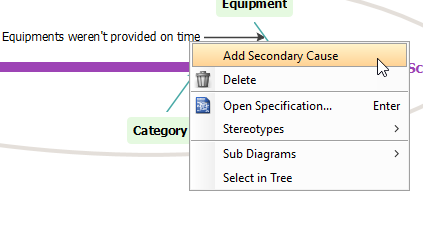
-
通过双击重命名次要原因。
-
重复上面的步骤5到8以创建更多主要和次要原因。
-
完成图表后,您将看到类似的内容:
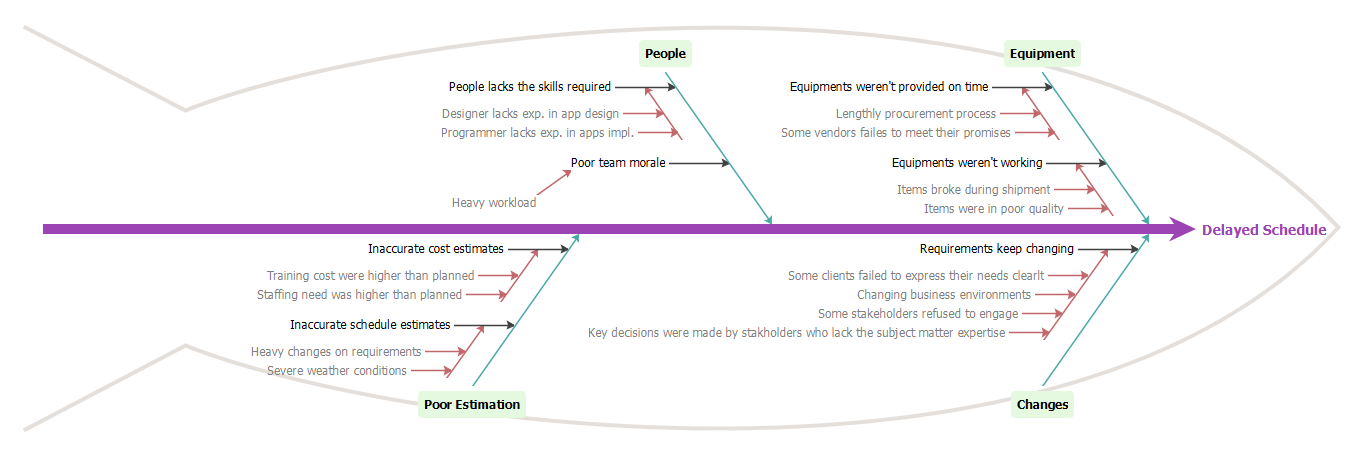
转载地址:http://qnbqz.baihongyu.com/
你可能感兴趣的文章
nodejs生成多层目录和生成文件的通用方法
查看>>
nodejs端口被占用原因及解决方案
查看>>
Nodejs简介以及Windows上安装Nodejs
查看>>
nodejs系列之express
查看>>
nodejs系列之Koa2
查看>>
Nodejs连接mysql
查看>>